A non-asymptotic model selection in mixture of experts models

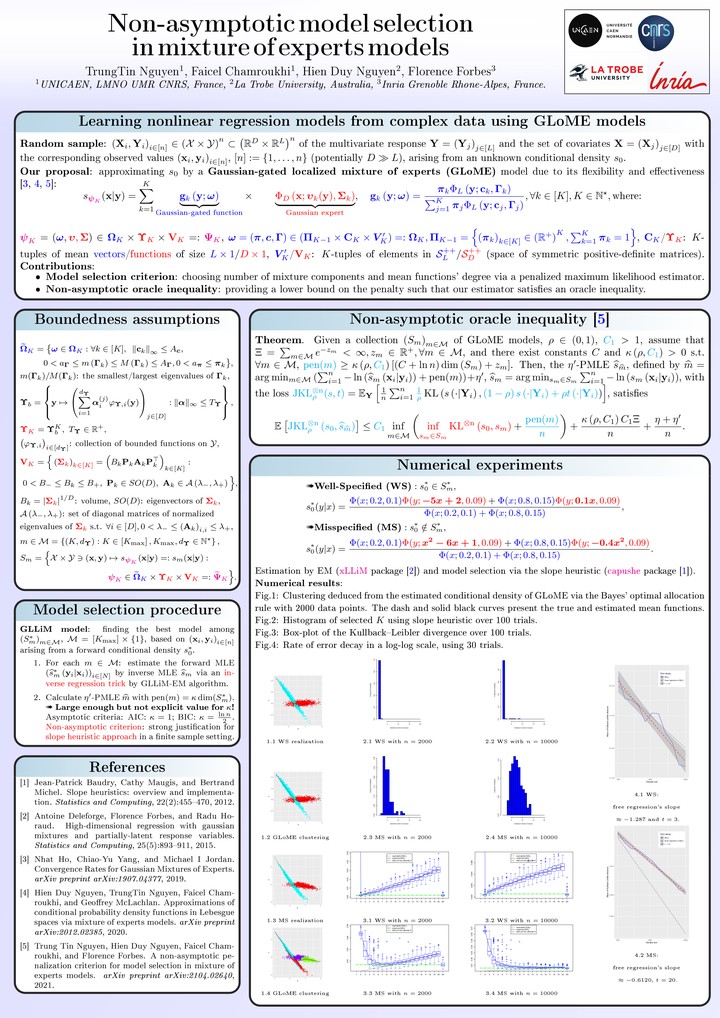
Abstract

Mixture of experts (MoE) is a popular class of models in statistics and machine learning that has sustained attention over the years, due to its flexibility and effectiveness. We consider the Gaussian-gated localized MoE (GLoME) regression model for modeling heterogeneous data. This model poses challenging questions with respect to the statistical estimation and model selection problems, including feature selection, both from the computational and theoretical points of view. We study the problem of estimating the number of components of the GLoME model, in a penalized maximum likelihood estimation framework. We provide a lower bound on the penalty that ensures a weak oracle inequality is satisfied by our estimator. To support our theoretical result, we perform numerical experiments on simulated and real data, which highlight the performance of our finite-sample oracle inequality.