Distance-based ABC procedures
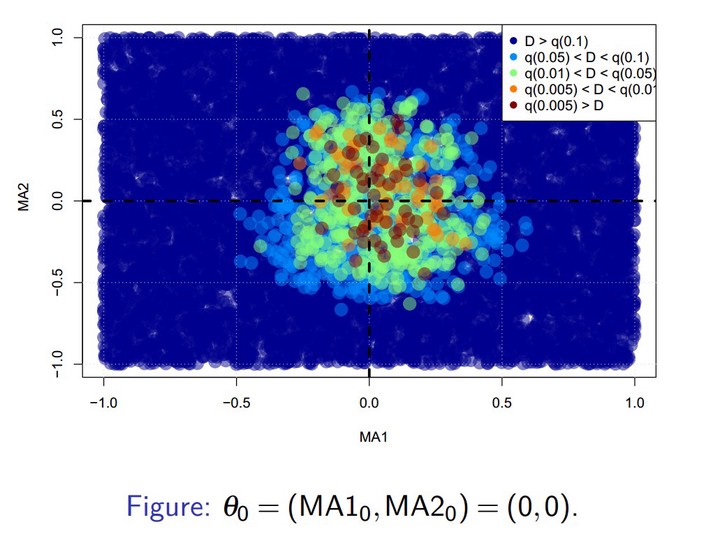 Image credit: Hien Duy Nguyen
Image credit: Hien Duy Nguyen
Abstract
Approximate Bayesian computation (ABC) has become an essential part of the Bayesian toolbox for addressing problems in which the likelihood is prohibitively expensive or entirely unknown, making it intractable. ABC defines a pseudo-posterior by comparing observed data with simulated data, traditionally based on some summary statistics, the elicitation of which is regarded as a key difficulty. Recently, using data discrepancy measures has been proposed in order to bypass the construction of summary statistics. Here we propose to use the importance-sampling ABC (IS-ABC) algorithm relying on the so-called two-sample energy statistic. We establish a new asymptotic result for the case where both the observed sample size and the simulated data sample size increase to infinity, which highlights to what extent the data discrepancy measure impacts the asymptotic pseudo-posterior. The result holds in the broad setting of IS-ABC methodologies, thus generalizing previous results that have been established only for rejection ABC algorithms. Furthermore, we propose a consistent V-statistic estimator of the energy statistic, under which we show that the large sample result holds, and prove that the rejection ABC algorithm, based on the energy statistic, generates pseudo-posterior distributions that achieves convergence to the correct limits, when implemented with rejection thresholds that converge to zero, in the finite sample setting. Our proposed energy statistic based ABC algorithm is demonstrated on a variety of models, including a Gaussian mixture, a moving-average model of order two, a bivariate beta and a multivariate g-and-k distribution. We find that our proposed method compares well with alternative discrepancy measures.